TIME VARIES WITH RELATIVE SPEED
Gary D. Evans
_____________________________________________________________________________
Experiment: Let a person sitting within a train-car measure the time it takes for a particle of light to travel between a held flashlight and a detector on the train's ceiling.
|
Let T1 = the time measured by the train rider performing the experiment.
Let T0 = the time measured by the observer of the same experiment standing outside the passing train.
Let v = the speed of train as measured by the outside observer as it passes by.
Let c = the speed of light
|
The lengths of the sides represented here are simply the (speed * time) = distances involved.
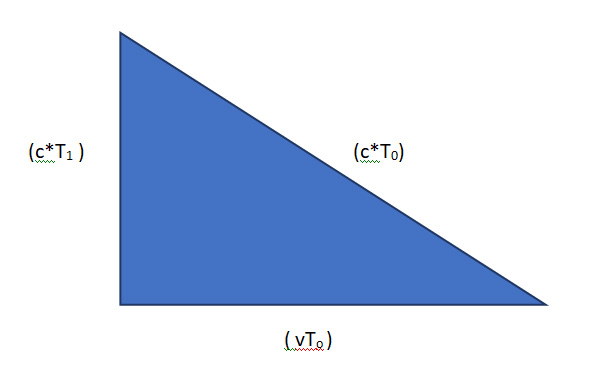
Pythagorean Theorm: for a right triangle, the length of the sides adjacent to the right-angle squared
and then added together will equal the length of the hypotenuse squared.
|
In this example: (c*T1)2 + (v*T0)2 = (c*T0)2
Square the values: c2T12 + v2T02 = c2T02
Rearrange: c2T12 = c2T02 - v2T02
Divide by c2: T12 = (c2T02 - v2T02) / c2
Simplify: T12 = T02 (1 - v2/c2)
Take the square-roots: T1 = T0(1 - v2/c2)1/2
|
CONCLUSION: As indicated by the final equation, as the speed of the train (v) approaches the speed of light (c), the value of the right side of the equation goes toward zero, meaning: as the speed of the train increases, the observer (wearing a T0 watch) sees the train-rider's T1 watch ticking ever more slowly. That is to say, the train-rider's rate of the passage of time is slowed relative to the outside observer's rate of time passage.
![]()
![]()
![]()
![]()