• Chapter 1 (00:00:00 - 00:21:54) INTRO
• Chapter 2 (00:21:55 - 01:17:35) EXPANSION
• Chapter 3 (01:17:36 - 02:19:13) CMB
• Chapter 4 (02:19:14 - 03:05:53) RECIPE FOR A HOT UNIVERSE
• Chapter 5 (03:05:55 - 03:44:57) THE FIRST THREE MINUTES
• Chapter 6 (03:44:58 - 04:05:30) A HISTORICAL DIVERSION
• Chapter 7 (04:05:31 - 04:36:52) THE FIRST ONE-HUNDREDTH SECOND
• Chapter 8 (04:36:53 - 04:46:38) EPILOG: THE PROSPECT AHEAD
• Chapter 9 (04:46:39 - 05:30:30) AFTERWARD: COSMOLOGY SINCE 1977    

1. INTRODUCTION
(table includes additions from other sources)

10^-43s

10³²K

10¹⁹GeV

Planck Time: Schwarzschild scale = horizon size. 11-dim. false vac. fluctuation seeds universe.

10^-38 - 10^-36s

10³²K

10¹⁹GeV

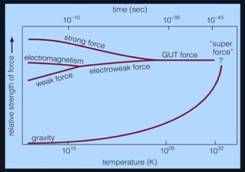
Gravity splits from metastable multi-dim. non-zero energy vac. field, w/ sufficient strength to convert directly into mass. Strong force next became distinct from EW, which then split into EM and weak force particles. All particles receded from each other simultaneously; at these high temps, kT ›mc2, all particles behaved as photons. Neutrino mass (Majorana): L-Handed neutrinos collided with Higgs yielding Massive R-handed neutrinos; then decayed back into L-handed low-mass neutrinos. (With later cooling, R-handed neutrinos decayed away.)

10^-36 - 10^-35s

10^-30cm

10²⁸K

Inflation Begins. Electroweak Epoch after strong force splits off;

10^-32s

10⁸cm

10²⁸K

10¹⁹GeV

Inflation ends - Between inflation’s start & before its end, the universe supercooled by ~10⁵ then reheated. Linear dims grew by at least 10²⁶, increasing volume by at least 10⁷⁸. (This would expand an object the size of one million-millionth the diameter of a 10^-15m proton to ~8cm in 10^-32s.

10^-30s

10¹²GeV

Speculation: Peccei-Quinn phase transition (if correct explanation for strong-CP prob.)

10^-20 - 10^-30s

›10²⁰K

TeV range

Strong force splits from the electroweak force; Baryogensis; Possible CDM split-off. (Note: Light travel time across a proton = 10^-23s.)

10^-9s

10¹⁵K

10¹⁵

GeV-TeV range

Electroweak phase transition (symmetry breaking). The Higgs mechanism: previously massless weak bosons W+, W-, and Z acquire rest mass; (all Higgs interacting particles acquire rest mass.) [Click here for an intuitive explanation of chiral symmetry breaking]

10^-6s

›10¹²K

GeV-TeV range

Quark-gluon plasma behaves as a fluid; b/anti-b asymmetry present; Neutron Threshold temp. = 10.903 x 10¹²K; Proton Threshold temperature =10.888 x 10¹²K

10^-6s

›10¹²K

100 MeV

Quark-Antiquark pairing. Temp. fell sufficiently to allow hadron/anti-hadron binding (mostly Pi-mesons). Muon pairs at ›= 1.23 x 10¹²K in thermal equil; soon the dominant form of baryonic matter. [Asymmetric decay channels for strange and charm quarks yielded matter over antimatter dominance (?energy level/time?)]

10^-5s

1-2x10¹²K

10¹²

150-200 MeV

QCD Phase Transition; Dark Matter freeze out. Baryon-antibaryon pair production followed by annihilations leaving 1BBP baryon excess. Quarks & gluons bind into baryons. (Axions produced, if they exist); p meson pairs produced at 1.57 x 10¹²K.

10^-4s

10¹²K

10¹¹

Annihilation of muons and pions. Hadron / anti-hadron pairs no longer produced.

2x10^-2s

10¹¹K

Mixture: ~10⁸⁹ of each elementary particle + 10⁸⁰P + 10⁸⁰N (1:10⁹ photons or e- or e+). Small #s of Neutrons and Protons now in equilibrium act as radiation with bT›mc².

›2x 10^-2s

3x 10¹⁰K

Equilibrium of e-, e+, photons, and neutrinos; 38%N/62%P

10^-1s

‹3x 10¹⁰K

6x 10⁹

3 MeV

Neutrino thermal equilibrium broken, i.e. decoupling. Weak force converts N to P.

1s

10¹⁰K

1+ MeV

Weak force no longer converting Neutrons to Protons // Lepton Epoch: lepton-antilepton pair production in thermal equilib.; leptons dominated ord. mass until temp fell (by 10s): pair annihil.

4s

5x10⁹K

4x10⁹

1.011 MeV

Radiation-Matter thermal equilibrium ending: e-/e+ annihil. = creat. (Ph. energy = 2 x 0.511MeV). 24%N : 76%P.

10s

4x10⁹K

10⁹

.0500 MeV

e-/e+ annihilations complete leaving 1 PPB matter remaining (from pairs originally present)

14s

3x10⁹K

4x10⁸

~100 KeV

Radiation › Matter Dominance Begins; Photons ‹511eV, e-/e+, ann. › creation. Reheating w/ neutrinos 8% cooler than e+/e-/photons. Du ann. = creation, i.e., bottleneck to synthesis of heavier nuclei.

  i.e., N:P now = 17%:83%

2-3mins

10⁹K

5x10⁸

70 KeV

Nucleosynthesis begins: D + 73%H + 27% 4He + trace 3He + trace 7Li. 10⁹ Photons+neutrinos to 1 e- after e+/e- annihilations releasing heat with photon energy 35% › neutrinos; Free neutrons decay into Protons with N:P now 14%:86%; Deuterium bottleneck continues.

4 mins

0.8x 10⁹K

3x 10⁸

Deut. bottleneck end (became stable). 87% P & 13% N. N cooked into 4He, eventually = 26% by wt.

35 mins

0.3x 10⁹K

10⁸

› 2 KeV

Nucleosynthesis ends. Photons 40% › energy than neutrinos.

1-5 days

2x 10⁷

2 KeV

Photons freeze out of thermal equilibrium. (Before this, interactions that changed photon #s proceeded rapidly as compared w/ expansion rate; w/ freeze out, CMB photons #s are now fixed.

› 1 year

› 9x10⁵

Compton scattering allows for thermal equilibrium no earlier than 1 year

??????

??????

‹ 10⁵

??????

Compton scattering ceases, decoupling matter and radiation.

40 years

4x10⁴K

1.4x10⁴

40eV

e- - photon collisions too weak to significantly change photon energies, only their directions. CMB spectrum unchanged (except for redshift) from this time.

10x10³ years

1.2x10⁴K

8.2x10³

1.0eV

Matter (mostly dark) density = Radiation density. CDM density perturbations grew while baryonic density perturbations could not, given its radiation pressure.

260x10³ years

3.1x10³K

1.3x10³

0.26-0.33eV

Recombination begins (thickness ~z = 900-1300, peaking at 1090 +/- 200). Dark matter perturbations continue to grow into gravitational wells.

384 x 10³ years

84x10⁶LY

3x10³K

1.09x10³

0.26eV

CMB-LSS: sufficiently cool to allow electrons and baryons to form neutral atoms. Free electron content dropped by 10⁴.

2.9x10³K

0.9x10³

Recombination fully ends Press. down by 109; (thickness from z~900-1200 w/ peak z=1091) & +/-200K

150x10⁶y

0.1-1.0x10³K

~23

0.01-0.10eV

Dark Ages End (Jeans Mass fell ‹= 10⁵ solar masses); first (pop3) stars & galaxies formed, reionizing the neutral atoms formed at recombination.

10⁹y

7

Small galaxies and galactic groups form

8x10⁹y

0.6

Dark and Baryonic matter equally dominant. Milky Way disk forms

9x10⁹y

0.4

Dark Energy domination over Matter. Accelerated expansion begins.

13.8x10⁹y

92x10⁹LY

2.72K(+/-0.002)

0

0.000691eV

Now: baryonic » photon energy [10⁹ ph x .000691eV = 691KeV to 1 nucleon = 939 MeV; neutrino background ~1.95K; Baryon# density p/mp = OB/mp*3H02/8pG = 1.1x10^-5 OBh2cm-3. 400 photons/cm3; 10¹³ photons/s/cm². Baryonic=4.9%; Dark=26.8%; Dark E.=68.3%

2. EXPANSION OF THE UNIVERSE

• 1750: Thomas Wright 1st conjectured that the Milky Way is a galaxy.
• Emmanuel Kant 1755: nebulae are circular galaxies.
• 1781 Messier Catalog of 103 objects (to avoid wasting time on anything but search for comets)
• 1890s: Supernovae observed and correctly interpreted.
• 1800-1900: Doppler, Spectral light (emission and absorption)
• The Milky Way: diameter 80,000 LY and thickness 6,000 LY, Halo 100,000 LY, Mass ›10¹¹ Suns, rotation 250km/sec, and the Solar System is about 30,000 LY from the center, and just North of the celestial equator.
• 1910-1920: Nebular light noted to be Doppler shifted to red (Virgo cluster red 1000 km/sec) or less frequently – blue
• 1923: Edwin Hubble resolved Andromeda into stars with the 100” Mt. Wilson Observatory telescope; found Cepheids Variables; discovered within the Milky Way and characterized into Apparent Luminosity vs. pulse period allowing for estimate of Andromeda’s distance at 900,000 LY, now known to be ~2,000,000 LYs.
• 1929: Hubble announced finding that the further away a galaxy – the greater the redshift (proportional).
• 1931: Hubble Const. meas’ed velocities up to 20,000km/sec finding proportionality held at 170km/sec per 106 Lys.
• 1936: Hubble Const. meas’ed velocities up to 42,000km/sec (0.14c) = 260x106 Lys – at limit of Mt. Wilson’s resolution.
• Data has been updated: 1/H (assuming H constant – which it is not) gives the age of the universe. (under 20 x 10^9 y). When gravitational attraction, slowing the initial expansion, the age estimate ~ 14 x 10^9 years which checks with ~age of our galaxy based on Uranium dating (U-235 : U-238).
• Size of the universe takes into account velocities and the expansion of space itself (z determines wavelength increase and distance to the object).
• 1917 de Sitter’s model showed redshifts and the expansion of space. As redshift data became accepted as indicating distances are expanding, Einstein - who had added a cosmological constant term to his Field Equations to stop GR from collapsing space under gravitation, accepted expansion and stated his cosmological constant had been an error. (Ironically the constant is now invoked to accelerate space under the discovery of Dark Energy.)
• 1922 Friedman modeled the universe’s expansion: closed, flat, open based on critical density which is proportional to H2 and, based on Hubble (at 15,000/106LY) = 5 x 10-30 gm/cc or 3 Hydrogen atoms per 1000L space.
• The galaxies are receding from one another because they were thrown apart at the beginning inflational event.
• Note: 1:08:00 --- Spherical Symmetry G.D. Burkolf 1923 – used to solve Friedman’s critical density. Escape velocity is the same for all galaxies! (The value is proportional to H2.)
• The size of the early universe increased proportionally to time 2/3 if the density of radiation is neglected, or to Time 1/2 if radiation density › matter density.

3. THE COSMIC MICROWAVE BACKGROUND (CMB)

• Beginning in the Spring of 1964 Penzias and Wilson used a Bell Telephone Labs 20’ horn telescope – designed for use with the earlier Echo Satellite. Despite cold soaking, comparing the differences across the sky, and other possible factors – excess noise reliably detected at the initially tuned wavelength of 7.35cm (4080 MHz) with a blackbody equivalent peak temperature of 2.5 - 4.5K). Penzias happened to telephone a fellow radio astronomer with Bernard Burke of MIT, who had just heard from another colleague, Ken Turner of the Carnegie Institution, who had recently heard a talk at Johns Hopkins given by P. J. E. Pebbles of Princeton about regarding an expected Blackbody spectral peak from the early universe peaking at ~10K. Burke, knowing of Penzias and Wilson’s work with the antenna asked how things were going. Penzias related the unexplained noise they were measuring and Burke suggested speaking with a group at Princeton who were working on a project at the time to detect photons of that approximate wavelength. In a 3/1965 preprint, Pebbles – having been influenced by Princeton’s Robert Dicke’s experimental work on microwave astronomy - reasoned that if the early universe contained an intense and short wavelength blackbody radiation during the early universe, that radiation would blast apart heavy nuclei as fast as they were formed. If blackbody spectrum did not exist at the time, nuclear reactions would have led to a significant proportion of heavy nuclei at the time, which did not occur. Pebbles calculated that the early blackbody spectrum would have redshifted down to something like 10K by now. Subsequent calculations around that time determined that the expected blackbody equivalent peak temperature would be closer to that actually observed. In 1964, the Princeton group including Dicke, Roehl, and Wilkinson began setting up receiving equipment and a small antenna on the roof of the Palmer Physical Lab at Princeton. Hearing of Penzias and Wilson’s findings – the two groups decided to publish two accompanying letters in “Astrophysical Journal” with Penzias and Wilson describing their findings and the Princeton group describing the possible significance. [Note: In the late 1940s, a Big-Bang theory of nucleosynthesis was posited by George Gamow, Ralph Alphers, and Robert Herman used by 1948 to calculate a background equivalent temperature of 5K. This same finding was calculated in the early 1960s independently by Soviet Union and by English researchers.]
• The CMB-LSS epoch was in thermal equilibrium as the number of interactions » expansion. During the 1890s, Max Planck worked out the blackbody spectrum at any temperature putting to rest the problem with the “Ultraviolet Catastrophe.” Energy is packetized and is inversely proportional to the wavelength.
• Typical chemical reactions involve transitions of ~ 1eV whereas typical nuclear reactions involve transitions on the order of MeV, which is why 1 pound of nuclear explosive will yield about 1 million pounds of TNT.
• Typical wavelength at 1K = 0.29cm and proportionately shorter with higher temperatures. Thus at room temperature of 300K, equivalent temperature= 0.29cm/300 = 967nm (infrared spectrum) whereas the surface of the sun = 5800K resulting in equivalent temperatures of those photons = 0.29cm/5800 = 500nm (visible spectrum) to which our visual system is tuned to perceive.
• CALCULATION OF RADIATION ENERGY DENSITY: The average distance between photons in blackbody radiation is ~= to the photon wavelengths. And, that typical wavelength is inversely proportional to the temperature, therefore the average distance between photons in a blackbody is also inversely proportional to the temperature. The number of things in a volume is inversely proportional to (their average separation)3. Therefore, in blackbody radiation the number of photons in a given volume is proportional to the (temp)3. The energy density per liter within blackbody radiation is: (photons/Liter)(average energy per photon) and the number of photons/Liter is proportional to the (temp)3, while the average photon energy is simply proportional to the temp. Therefore, the average energy per liter in blackbody radiation is proportional to (temp)4. Quantitatively the energy density of blackbody radiation is 4.72eV/L at 1 deg. K. This is known as the Stephan Boltzmann Law. Thus, the CMB bathing us now has an energy density of approximately 4.72eV/L x 34 = ~380eV/Liter. And, at the time of the CMB-LSS, when the temperature was 1000 times higher the energy density was therefore 10004 higher or 1012 times the current value = ~380 x 10¹²eV/Liter.
• When the universe had cooled to 3000K the density of photons that could dissociate hydrogen atoms had dropped off sufficiently to allow a sufficient combination of free electrons and protons to form hydrogen, broke the thermal equilibrium between radiation and matter, clearing the path for photons to move out without significant scattering. Those photons (about 1um at the time with an average distance between photons also 1um) now bathe the universe in the blackbody spectrum frozen in at that time and temperature, now stretched by 1000x to 1mm wavelengths with photons about 1mm apart.
• Since 1965 the intensity vs. wavelength data of the CMB-LSS has been repeatedly investigated at increasingly finer resolution and multiple wavelengths (73.5cm – 0.33cm on Earth, and via a cloud of interstellar CN gas with absorption seen at 0.3875 x 10-4cm corresponding to a rotating state induced by ~3K CMB photons), agreeing perfectly with the expected blackbody values including those within the short wavelength side of the curve.) Balloon, rocket, and satellite results (COBE, WMAP, and Planck) show perfect agreement.
• The Earth rotates around the sun at ~30km/sec, and the sun rotates around (with) the galaxy at ~250km/sec.
• CALCULATION OF RADIATION ENERGY DENSITY (CONTINUED): As above, at any given temperature, the number of photons present per unit volume is inversely proportional to the (wavelength)3 and directly proportional to the (temp)3. For a temperature of 1K there would be 20,282.9 photons / liter. Therefore, at 3K, there are 550,000 photons / Liter. The current density of nuclear particles (neutrons and protons) = 0.03 – 6.0 particles per 1000 Liters with the upper limit at twice the critical density. Thus, there are between 108 and 2 x 1010 photons for every nuclear particle in the universe today, or a ratio of about 1:109 and this ratio has been maintained since the CMB-LSS.
• Gravitation of a clump increases with the size of the clump, while radiation pressure, acting against the clumping, does not depend on the size. Therefore, for any size of a mass, there is a size threshold that will allow clumping – known as the Jeans Mass (1902 – Sir James Jeans), which is proportional to the (pressure)3/2. At the CMB-LSS epoch, the radiation pressure was enormous and the Jeans Mass was correspondingly large (about 106 times the mass of a large galaxy), therefore no large clumping occurred. Pressure is proportional to the number of particles generating the pressure, and as free electrons and protons combined to form atomic hydrogen, radiation pressure dropped by a factor of ~109. And, the Jeans Mass then fell to (that factor)3/2 or (109)3/2 to about 10-6 the mass of a typical galaxy. From then on, large scale clumping could occur.
• As a consequence of the number of photons vs. matter particles (10⁹:1), there was an epoch when radiation energy exceeded the energy held within matter particles. The energy held within the mass of a nuclear particle is given by E=mc2 = ~939 MeV. The energy of an average CMB-LSS photon (3000K) = 0.0007eV so that even though the ratio of photons to matter = 10⁹, most of the energy of the current universe is in the form of matter – not radiation. But, when the average photon energy was much greater, in an earlier epoch, the energy of the average photon equaled the energy within an average nucleus. Because of the 10⁹:1 numerical ratio, in order for blackbody photons of the early universe to exceed the energy of a typical nuclear particle, the photon required 10^-9 the energy of that typical nuclear particle mass, or ~1eV, which occurred when the temperature was about 1300 times greater than at present, or ~4000K. This temperature marks the boundary between the early radiation dominated era and the current mass dominated era (where most of the energy is held within the mass of nuclear particles). Exactly why the universe would have moved from radiation domination to mass domination at about the same time as when the universe moved to transparency to radiation is unknown. If the ratio of photons to nuclear particles was 10x greater, i.e. 10¹⁰ instead of 10⁹ then radiation domination would have continued until the universe fell to a blackbody temperature of 400K, well after the universe became transparent at 3000K. The enormous dominance of photons to the total energy density has fallen due to the expansion, whereas the density of matter particles has remained unchanged and thereby dominates our current universe.

4. RECIPE FOR A HOT UNIVERSE

• As the universe expanded, radiation wavelengths lengthened and the blackbody spectrum cooled to lower temperatures with a shift to longer wavelengths. The lower temperatures then drove the temperature of matter particles. Going backwards, as temperature increased, photons eventually had sufficient energy to spontaneously transform to directly to matter and antimatter particle sets.
• Photon Energy = kT, where k = Boltzmann’s Constant = 8.627x10-5eV/0K. (At 3000K an average photon then = 0.26eV.)
• For a photon to have sufficient energy to yield the creation of a matter particle with rest energy E=mc2 one can set kT=mc2 or T = mc2/k. Thus, there is a characteristic temperature where photons can create specific particles – each with their own rest energies. As an example, electron:positron pairs have rest energies of 511KeV each and can therefore be created out of a collision with 2 photons – each having energies of 511KeV. As T=E/k, this yields a temperature of 6 x 109K. At that temperature, photons and electron:positron pairs would be in thermal equilibrium. Moving up the mass scale, muon+:muon- pairs have rest energies of 105.6596MeV yielding a creation temperature of 1.2 x 1012K. [See Table 1 for complete list of particles and characteristic temperatures]
• Note that in counting up the number of particles contributing to radiation pressure of the early universe, particles and antiparticles are statistically considered as separate particles as are otherwise identical particles with differing spin states such as electrons and photons, finally the electron must follow the Pauli Exclusion Principle which results in their contribution to the total energy density reduced by a factor of 7/8ths. [See Table 1 for all species.]
• Again, the energy density of the universe is proportional to Temp4 and to the effective number of particle species whose threshold temperatures are below the temperature of the universe. To determine the expansion rates all that is needed is the temperature as that will determine the energy density and hence radiation pressure vs. gravitational attraction of all the particles existing.
• To determine the time required for the energy density to fall from one value to another: it is proportional to 1/(energy density at temp-1)1/2 - 1/(energy density at temp-2)1/2 and, as energy density is proportional to Temp4 and to the number of species present, the time difference between two temperature periods (if no species production thresholds are crossed) is proportional to (1/Temp22 - 1/Temp12). For example, if beginning at a temperature of 108K it took 0.06 years = 22 days for the temperature to drop to 107K, then another 6 years to drop to 106K, then another 600 years to drop to 105K, … adding up the entire cooling process to the CMB-LSS it took ~700,000 years.
• Energy Density of radiation approximated the energy density of matter at about 4000K
• Thermal Equilibrium conserves total energy therefore once the quantities were defined, they have remained unchanged. There are believed to be just three fundamentally conserved quantities: 1) electric charge; 2) baryon number; 3) lepton number (of which there are two [? Three including the tau] types: electron lepton number and muon lepton number). To specify the state of the universe – must consider their numbers per unit volume and temperature at any given time. These values vary with 1/(univ.size)3. This same relationship holds for the number of photons. As seen above, the numbers of photons per unit volume is proportional to the T3 and the temperature varies with 1/(univ.size). Therefore, the total electric charge, baryon number, and lepton number per photon remains fixed and the state of the universe of those numbers can be calculated by the photon numbers. Note that the more accurate quantity to consider is not the actual photons/unit volume but rather entropy/unit volume, but as a practical matter – photon numbers can be used in any calculations – see table for entropy relation (effective number of species) to specific varieties of particles.


Particle Types Rest Energy Threshold Temp. Effective # Species Mean life (secs) Photon part = antipart 0 0 1x2x1 = 2 stable Neutrinos electron 0 0 2x1x7/8 = 7/4 stable “ muon 0 0 2x1x7/8 = 7/4 stable “ tau 0 0 2x1x7/8 = 7/4 stable Electron e+ / e- 0.5110 5.930 2x2x7/8 = 7/2 stable Muon u+ / u- 105.66 1226.2 2x2x7/8 = 7/2 2.197 x 10-6 Pi Mesons π0 134.96 1566.2 1x1x1 = 1 0.8 x 10-16 “ π+, π- 139.57 1619.7 2x1x1 = 2 2.60 x 10-8 Proton p, anti-p 938.26 10,888 2x2x7/8 = 7/2 stable Neutron n, anti-n 939.55 10,903 2x2x7/8 = 7/2 920


• The Cosmic Charge per Photon is 0. The baryon number per photon = 10-9 indicating the matter – antimatter excess ratio. Observational evidence strongly suggests that there are no regions within the universe where this relationship is reversed, thus there is a true small imbalance.
• Lepton number density in the current universe: 1) charges are entirely balanced in the current universe: 1 positive charged proton per 1 negatively charged electron; 2) ~87% of nuclear particles in the present universe are protons; 3) the number of electrons is ~ the number of (“nuclear particles” stated – expect he meant:) protons; 4) The neutrinos and the antineutrinos carry no charge but a lepton number of 1 and -1 respectively. Therefore, to determine the total lepton number, the difficult to detect neutrino must be included. It is assumed - but by no means certain - that the lepton number per photon corresponds to the baryon number per photon (1 part in 10-9). Given neutrinos interact so weakly, they may have escaped self-annihilation resulting in the number of neutrinos and their antiparticle species being close to equal and their total number being close that of photons.
• Recipe for the early universe: take the charge per photon = 0, Baryon number 1 part in 109 of photons, Lepton number uncertain but small, take the temperature at any given time as proportional to the size of the universe at that time to the current time multiplied by the current temperature of 2.72K. At any given time and temperature, the various components will follow the rules of thermal equilibrium for each of the components. The expansion will be governed by the gravitational force generated by the components [+ dark energy].
• Above 1.5 x 1012K the universe would contain high numbers of pi-mesons, weighing about 1/7 of a nuclear particle. They react strongly with each other and with nuclear particles and is responsible for most of the attractive force that holds nuclear particles together. Those complex interactions make it difficult to calculate the behavior of matter at those super-high temperatures.

5. THE FIRST THREE MINUTES

• Beginning at 1/100 second – at temperature of 10¹¹K. Despite expansion, the universe is in a state of nearly perfect thermal equilibrium. The conserved quantities: charge, baryon number, lepton number are all very small or equal to zero. Abundant particles are those whose thresholds are below 10¹¹K: Electrons, positrons, photons, neutrinos, and antineutrinos. They remain at thermal equilibrium and, as they are so far below their threshold values, they all behave as various types of radiation. Calculating their energy densities, referring to table 1 again:


Particle Types Effective # Species Photon part = antipart 1x2x1 = 2 Neutrinos electron 2x1x7/8 = 7/4 muon 2x1x7/8 = 7/4 tau 2x1x7/8 = 7/4 Electron e+ / e- 2x2x7/8 = 7/2


• Electrons + positrons contribute 7/4’s [ (7/2) / (2) ] as much energy as do the photons, and the neutrinos + antineutrinos contribute the same as the electrons + positrons [NOTE: the book does not mention tau neutrinos… so, there appears to be an additional 7/4 to take into account.] So, the total energy density is greater than the energy density for pure electromagnetic radiation by a factor of 7/4+7/4+1 = 18/4 = 9/2. The Stefan Boltzmann Law gives the energy density of electromagnetic radiation at a temperature of 10¹¹K as 4.72 x 10⁴⁴ eV/Liter. So, the total energy density of the universe at this 10¹¹K was 9/2 times as great or (4.72 x 10⁴⁴) x (9/2) = 21 x10⁴⁴ eV/Liter, which equals a mass density of 3.8 x 10⁹Kg/Liter or 3.8 x 109 times the density of water under normal terrestrial conditions (relating mass to energy by E=mc2). If Mount Everest were made of this matter of this density, its gravitational attraction would destroy the earth!
• The characteristic expansion time for the universe at the temperature of 10¹¹K is ~0.02 seconds, where the characteristic expansion time = 100 x length of time in which the size of the universe would increase by 1%. The characteristic expansion time of any epoch = 1/H, where H = the Hubble Constant at that epoch. The age of the universe is always less than the characteristic expansion time because gravitation is continually slowing the expansion.
• There are a small number of nuclear particles at 10¹¹K = ~1 nuclear particle per 109 photons, or electrons, or neutrinos. The neutron is heavier than the proton with a mass difference between them of 1.293 MeV. At this temperature, the characteristic energy of electrons and positrons is much larger at about 10 MeV (by Boltzmann’s Constant x temperature), thus the rapid collisions between protons, neutrons, and the much more numeroius electrons, and positrons, etc., caused rapid transitions from protons to neutrons and neutrons to protons. The most important reactions at this temperature are: anti-neutrino + proton  positron + neutron (along with the reverse reaction) and neutrino + neutron  electron + proton (along with the reverse reaction).
• Given the assumption that the net lepton number and charge per photon are very small, there are almost as many neutrinos as antineutrinos and as many positrons as electrons so the numbers of transitions from N-P = P-N. There are many possible sizes of the universe at 1011K – ranging from 4LY to nearly infinite in size.
• Over a period of ~0.11 secs, the universe cooled by about 3x to ~3x10¹⁰K. Thermal equilibrium between photons, electrons, positrons, neutrinos, and antineutrinos continued, and energy density fell as Temp4 to 3x107 gm/cc. The rate of expansion fell as Temp2 with the characteristic expansion time to 0.2 seconds. Easier for N-P than P-N, thus now 38% neutrons and 62% protons.
• 1.09 seconds after the temperature = 10¹¹, the temperature fell to 10¹⁰K. The mean free path of the neutrinos has increased to the point where they were no longer in thermal equilibrium with other particles - behaving as free particles. Before decoupling, the typical neutrino wavelength was proportional to 1/temp and since the temperature fell off by 1/(size of the universe), the wavelength increased proportional to the size of the universe. The total density continued to fall as temp^-4 now equaling 3.8x10⁵ gm/cc. Characteristic expansion time now = 2 seconds. The temperature now is only twice that of the threshold temperature of electrons and positrons so they are just beginning to annihilate faster than they can be created out of radiation. The N:P ratio now at 24%N:76%P.
• 13.82 seconds after the temperature = 10¹¹K, the temperature had fallen to 3x10⁹K. The threshold was now below that of electrons and positrons therefore annihilations rapidly proceeded resulting in reheating of colliding particles. As neutrinos received none of the heating, they were then 8% cooler than electrons, positrons, and photons. From this period on, the temperature of the universe refers to the temperature of the photons. At the lower temperature, Helium nuclei could formed remain stable. This began as a slow process given the ongoing such rapid expansion that nuclei can only be formed under fast two body reactions: proton and neutron to Deuterium nucleus with the released energy carried away by a photon. The Du nucleus can then: 1) collide with a proton forming He-3; 2) collide with a neutron to form H-3; and finally, He-4 can be formed either from a collision between H-3 and a neutron, or between H-3 and a proton. In any of these cases, the Du nucleus must first be formed and remain stable, despite its relative weak bonding as compared with H-3, He-3, or He-4. At this temperature, Du nuclei are destroyed as fast as they are created – hence forming a bottleneck to the production of heavier nuclei. Balance of N:P now = 17%:83%.
• At 109K the universe is about 70x hotter than the Sun’s core. Elapsed time from 10¹¹K = 3m2s. e+/e- annihilations have mostly completed, leaving photons, neutrinos, and antineutrinos and the released energy caused the photons to have 35% more energy than the neutrinos. He-3, He-4, and H-3 are now stable but Du bottleneck still present. In each 100 seconds to follow 10% of the remaining neutrons decay into protons. The N:P balance is now 14%:86%. At a temperature, just under 10⁹K, Du becomes stable breaking the bottleneck and allowing heavier nuclei to form rapidly, but with other bottlenecks, nuclei larger than He-4 do not form in large numbers. (There are no stable nuclei with 5 or 8 nucleons, thus nearly all of the remaining neutrons are cooked into He nuclei.
• 3min 46sec after the temperature had equaled 1011, the temperature had fallen to 0.9x109K. The N:P had fallen to approximately 13%:87% at which point nucleosynthesis continued. Essentially all the neutrons are cooked into helium with the fraction of helium equal to the fraction of all particles bound into helium – half of which are neutrons so the fraction by weight of helium equals twice the fraction of neutrons among nuclear particles (2 x 13%) or 26% (max 28% if nucleosynthesis proceeded a little earlier).
• 34m 40 sec after the temperature had equaled 10¹¹, the temperature had fallen to 3x10⁸K. e-/e+ annihilations had by then concluded, leaving 1:109 electrons – just enough to balance the positive proton charge. The annihilations have permanently left photons with a 40% higher energy than the neutrinos. Energy-mass density = 9.9% of water, of which 31% is in the form of neutrinos and antineutrinos, and 69% in the form of protons. Expansion time = 1h 15m. Helium now 22-28% by weight plus free protons. There is 1 electron for each free or bound proton.
• By 700,000 years [now known to be 380,000 years] – the universe was sufficiently cool to allow atomic hydrogen to form and for photons to achieve long free paths resulting in the CMB-LSS.
• The decoupling of matter and energy thereafter allows the formation of the first stars and galaxies.
• In 1967 Wagoner, Fowler, and Hoyle calculated DU abundance based on the number of photons per nuclear particles in the early universe and found it was very sensitive to that parameter:


Photons/nuclear particle = 10⁸ ? Du PPM = 0.00008 = 109 ? Du PPM = 16 = 1011 ? Du PPM = 600


• If we determine the primordial abundance of Du – before stellar processes began, the photon : nuclear particle ratio could then be deduced, and knowing the present blackbody temperature of 3.72K, the present nuclear mass density could be calculated and thereby determine whether the universe is open, closed, or flat. However, it is difficult to determine primordial Du abundance. The Du content by weight of earth’s water is 150 PPM, but this biased by its weight being twice that of hydrogen and making it more likely to be bound into molecules (heavy water) than simple hydrogen being bound into ordinary water so as the earth formed a smaller amount of Du than hydrogen would have escaped the earth’s gravitational field – yielding a higher PPM content in earth’s oceans today than that within the primordial epoch. On the other hand, spectroscopy yields only a very low Du abundance on the surface of the sun, less than 4 PPM, but this too is biased: Du in the Sun’s outer atmosphere would have been burned into He-3. In 1973, cosmic deuterium abundance was more firmly determined by the ultraviolet detecting satellite Copernicus. By characterizing the absorption lines of interstellar clouds as stellar radiation passes through, the relative abundance of H:Du can be determined without bias found to be ~20 PPM by weight of Du, indicating 1.1 x 10⁹ photons per nuclear particle. The current temperature of 2.72K indicates that there are currently 550,000 photons/liter therefore there are 500 nuclear particles per 10⁶ liters in the current universe, which is considerably less than the 3000 nuclear particles per 106 liters required to close the universe. Weinberg indicates this is an unconvincing argument given Deuterium we see now could have been relatively recently produced – yielding a speciously high value and thus indicating a too low nuclear particle per photon tally. On the other hand, the current helium abundance is a better measure as we would have signals if it was created more recently in significant measures.
• As above, neutrinos were freed from thermodynamic equilibrium as the temperature dropped to below 1010K. Since that time neutrino wavelengths have expanded with the expansion of the universe, and their blackbody temperature has been unaffected by processes since their creation. There should be 10⁹ neutrinos and antineutrinos per every nuclear particle in the universe, and their temperature should be slightly less than photon temperature given they were not affected by the reheating of the annihilation of e-/e+ pairs in the early times. The temperature difference should be (4/11)3 or 71.38%. [hear 3:38:33] The neutrinos and antineutrinos thus contribute 45.42% the energy of photons in the current universe. The neutrino temperature predicts that 71.38% of the photon temperature should be 2.72K x 0.7138 = ~2.0K.
• The remaining question is whether the lepton temperature is small – as above. Lepton number = number neutrinos and other leptons - number antineutrinos and other antileptons. If the lepton number density is as small as the baryon number density, then the number of neutrinos and antineutrinos should be equal to each other, to 1 part in 10⁹. On the other hand, if the lepton number density is comparable to the photon number density, then there would be a degeneracy – either an appreciable excess of neutrinos and deficiency of antineutrinos, or an excess of antineutrinos and a deficiency of neutrinos. Such a degeneracy would affect the shifting neutron: proton balance in the first three minutes and hence would change the amounts of helium and deuterium generated in the early universe. The detection of a 2K neutrino blackbody would settle the lepton number question and would point to the standard model as being accurate. But, despite there being 10⁹ neutrinos per nuclear particle, their detection remains quite difficult. [QUESTION: HAS THE NEUTRINO BACKGROUND BEEN DETECTED TO DATE IN 2017].
• A question remains as to whether the very early universe was isotropic and homogeneous or whether it was not and was only later smoothed out by frictional forces within the expanding universe. Charles Meisner of the University of Maryland has advocated a “mix-master” view – that the very early universe was significantly inhomogeneous and anisotropic, and further that the frictional heat of the homogenization process resulted in the excess photons over nuclear particles that we see. There are no theorized mechanisms that could have led to such inhomogeneous and anisotropic times, and there is no mechanism known to calculate the frictional heat that would have been generated from the proposed smoothing. In addition, we really do not know whether we exist in a particular area of the universe that has always been homogeneous and isotropic with other regions being otherwise.

6. HISTORICAL DIVERSION 1940s - 1970s

• Long before 1965 – from the 1940s to the 1950s, from the then known ~20-30% helium and 70-80% hydrogen it would have been possible to calculate that nucleosynthesis had to have begun at a time when the neutron fraction of nuclear particles had dropped to 10-15%. Further, the current helium abundance by weight being twice the neutron fraction at the epoch of nucleosynthesis, could have led to a calculated temperature of 10⁹K at the time. Then, knowing that nucleosynthesis would proceed at those temperatures, the nuclear particle density could have been calculated, and the photon density to thus be calculated from the known properties of blackbody radiation. The ratio of photons : nuclear particles at the time of cosmic nucleosynthesis would thus also have been known. As that ratio remains fixed, observation of the density of nuclear particles in today’s universe would have led to an approximation of the current density of photons, which would have led to the calculation of a CMB-LSS blackbody radiation peak of between 1 and 10 degrees K. In fact, such a calculation did proceed in 1948 but did not lead to a search for the radiation. In the late 1940s – a Big Bang cosmological theory was being explored by George Gamow, Ralph Alpher, and Robert Herman. They assumed that the universe began as pure neutrons, and that they began to convert to protons through the familiar radioactive decay process (N - P + e- + anti-v). As the universe expanded and cooled, heavier elements could be rapidly synthesized by a series of neutron captures. They calculated that to generate todays light elements, the photon:nuclear particle ratio should be ⁹. Using an estimate of today’s nuclear particle density, they were able to calculate a blackbody radiation that should exist currently as 5K. This was a close guess, but we know that the universe began with an equal number of protons and neutrons, and that neutron to proton conversion and nucleosynthesis involved multiple particles, not through beta-decay of N to P. These facts became known in the 1950s and the correct calculations were made by 1953. It took, however, another 10 years for this line of reasoning to lead to a calculation of the expected blackbody radiation – by three independent groups in Russia, England, and Peebles in the US. By that time, Penzias and Wilson had already begun their studies in New Jersey, discovering an excess noise in their antenna and receiver which they could not explain, leading to a conversation with the Dicke group at Princeton and the joint publications of their observation and the Princeton group’s theoretical analysis of it.
• Hans Suess and Harold Urey calculated back in 1960s that the universe contained approximately 75% hydrogen by weight, that could only have been produced in the very early universe. This by itself indicates that the ratio of photons to nuclear particles had to be quite large in order to keep all the hydrogen from cooking into helium and the heavier elements at those times.
• It became technologically possible to detect a 3K blackbody radiation background in the mid-1940s to the 1950s. In 1946, a team at the radiation laboratory at MIT, led by Robert Dicke, calculated that any extraterrestrial background would have to have a temperature of less than 20K, as based on observations of atmospheric absorption.
• There are many reasons why there was a delay in searching for CMB blackbody radiation.

1. The mechanism of synthesis of the heavier nuclei had not been fully worked out. In 1952 Salpeter did show that the known gap at nuclei with five or eight particles could be bridged in dense stellar helium-rich stellar cores by the collision of two helium nuclei which could create an unstable isotope of beryllium (Be8), which under the high-density conditions, could then collide with another helium nucleus before decaying, producing a stable carbon-12 nucleus. A few years later, in 1957 Geoffrey, Margaret Burbidge, Fowler, and Hoyle showed that heavy elements could be built up in stars, especially in supernovas and the like during periods of intense neutron flux. Hans Bethe and others showed during the late 1930s and early 1940s that stellar fusion proceeded via a complex fusing of 4 protons, but astrophysicists noted that the idea that helium was all created within stars led to calculations of too much energy being released thereby. In 1964 Hoyle and R.J. Tayler calculated that such helium abundance could only have been created within a Big-Bang process. 2. There was insufficient communication between theorists and experimentalists – the theorists were not sufficiently aware of the developing field of radio-astronomy, and experimentalists were not sufficiently aware of the developing field of cosmological theory. 3. It appears that physicists had difficulty in taking seriously any theory of the early universe, let alone a Big-Bang model.

7. THE FIRST ONE-HUNDREDTH SECOND

• At temperatures exceeding 10¹¹K (before 0.02 seconds), the short-range strong-force interactions, those at ~10^-13 cm, became significant. When two protons are pushed sufficiently close together, their strong-force interaction becomes ~100 times greater than their electrical repulsion – which explains why strong interactions are able to hold together nuclei containing ~100 protons against their mutual electrical repulsion (pg. 135).
• In calculating electromagnetic scattering of electrons, the Fine Structure Constant = 1/137.036 is used as a factor in calculating the contribution of individual possible processes within a Feynman Diagram of interactions. Complicated diagrams therefore give only small additional contributions over simple ones, and the scattering process can be accurately estimated. With strong interactions, however – those involved with hadrons - the equivalent constant is equal to ~1 resulting in complex diagrams generating large contributions compared with simple ones, making estimates very difficult to achieve. This has been the most difficult problem in particle physics.
• All hadrons are below their threshold temperatures at 10¹¹K. The lightest of the hadrons, the pi-meson has a threshold temperature of 1.6 x 10¹²K.
• All hadrons are composites of fundamental particles – the quarks, as posited by Murray Gell-Mann and independently by George Zweig, both of Cal Tech. Quarks come in six different flavors (up, down, strange, charm, top, bottom) and each flavor comes in three colors. The force between quarks is governed by a maximum bond length between them. When energy stretches that bond length to just beyond its maximum, sufficient energy is localized to then create quark pairs, each bonding to the “separated” original quarks, thus maintaining that maximum bond length. In other words, there can be no free quarks, but quarks operating below that maximum bond length, at a sufficiently high energy density / temperature (at about 0.01 seconds) have complete freedom of movement. If the average energy content of a volume increases sufficiently, quarks will behave as individual particles having asymptotic freedom (a non-Abelian gauge theory).
• Weak force interactions involve energies of about 10^-7 of the energies involved in electromagnetic interactions, yet they are united under a field theory proposed by Weinberg in 1967 and Abdus Salam in 1968 in which neutral currents are invoked and observed 6 years later in 1973. As is true of the strong force, the weak force involves non-Abelian gauge theory. Gauge theories in general may well point the way to full unification of the forces. These theories exhibit a phase transition at a “critical temperature” of about 3 x 10¹⁵K, above which there is an essential unity between weak and electromagnetic interactions, and where they both exhibit the inverse-square relationship and each operates at about the same strength. Below that critical temperature, a loss of symmetry was manifest.
• Gravitational forces within the early universe were vanishingly weak. The gravitational interaction between a hydrogen atom’s proton and electron is only 10^-39 that of the electromagnetic interaction. Nonetheless, there may have been an epoch when all the forces operated with equivalent strength during interactions. For example, the Earth revolves around the sun a little faster at its current temperature than if it were cooler, as its heat involves photons that add to its gravitational strength and hence to our orbital speed. At extremely high temperatures – calculated as about 10³²K at about 10^-43 secs, the energies of the particles in thermal equilibrium would become so large that the gravitational forces between them would be as strong as any of the other forces. At that temperature, the “horizon” – the distance beyond which it is impossible yet to have received any signals would be closer than one wavelength of a typical particle in thermal equilibrium – i.e. each particle would be about the size of the observable universe. It is at that temperature 10³²K that gravitation was last in thermal equilibrium with the other contents of the universe. Since that time, the effective temperature of the gravitational radiation has dropped in inverse proportion to the size of the universe. There might well be a blackbody spectrum of that gravitation existing today at a temperature of ~1K.

8. EPILOG: THE PROSPECT AHEAD

• Brief view of omega greater than 1 and less than 1 futures and of an oscillating universe, referencing the Dicke group’s 1965 paper regarding an oscillating universe and the expected blackbody radiation signature from the last “bounce.”
• “The effort to understand the universe is one of the very few things that lifts human life a little above the level of farce, and gives it some of the grace of tragedy.”

9. AFTERWARD: COSMOLOGY SINCE 1977

• Hubble constant variably recorded at between 40–80 km/sec/megaparsec as of 1993.
• Nov 18, 1989 COBE launched and within the first 8 minutes detected the intensities fit a blackbody curve at 2.735K, and after data processing and further data collection, anisotropies found to equal ~30 x 10^-6K across angular scales between 7 and 180 degrees. These were generated by gravitational irregularities in the early universe encoded into the CMB-LSS.
• Observation of spiral galaxy motions is consistent with the presence of dark matter in a dark halo surrounding galaxies.
• An omega = 1 requires ~10^-29gm/cc density for a Hubble constant of ~80km/sec/megaparsec. Galaxies contribute about 40% of that critical value. Given the abundances of the primordial elements, we know that the ratio of photons to nuclear particles is ~10⁹:1. Therefore, dark matter cannot be counted as the same material as make up the nuclear particles. Thus, with a Hubble constant of ~80, normal mass contributes only about 4% of the critical mass.
• Observations over the past few decades show that small CP violations in weak and electromagnetic interactions do occur at a temperature of ~10¹⁶K, and can account for the matter-antimatter inequality, at a level of approximately 1 part in 10⁹.
• CERN experiments in 1990 confirmed through the decay of Z0 particles that three species of neutrinos exist and is consistent with primordial nucleosynthesis calculations.
• Other dark particles could include supersymmetric partners, axions, etc. and vacuum energy which leads to vacuum mass densities too large by 10¹²⁰ times!
• Vacuum energy works exactly as does Einstein’s cosmological constant (the only term that can be added to the field equations that does not violate the equivalence of coordinate systems). There is no known method to fix the value of a cosmological constant, but the Anthropic Principle would explain its selection in our universe.
• We know that gravitational clumps had begun to form when the universe was 6x smaller than its present size, when the density of ordinary matter was 63 = 216 times larger than present, and at a time when a net vacuum mass density would have had no effect on those clumps unless it were at least ~100 times larger than the present cosmic density of ordinary matter. A smaller vacuum mass density could have interfered with the formation of galaxies at later times, but a net vacuum mass density about 10-20 times the present density of ordinary mater would have left plenty of time for galaxy formation. The anthropic principle, therefore, provides no reason why a positive net vacuum mass density should be smaller than about 10^-20 times the present mass density of matter (including whatever dark matter is present in galaxies and clusters of galaxies). Is it possible that 80-90% of the critical mass arises from the vacuum, with the remainder made up of ordinary matter (mostly dark) of one sort or another?
• If vacuum energy is a major contributor to the mass density of the universe today then, given its density remains constant as the universe expands, and therefore its contribution would have been less in the past, whereas ordinary matter (and dark matter?) becomes less dense with expansion, observations of cosmic evolution would remain consistent with theory.
• Inflation explains flatness, isotropy, and the horizon problem and is consistent with observation. String theories, of which there are more than 1000, integrates gravity in a larger framework with forces unified at the 10³²K scale. (There was no mention as of the time of this updated book’s publication in 1993, of potential B-field polarizations as possible proof of inflation.)